PPML Summer School: Python Overview

The purpose of this notebook is to help you setup the environment for python data analysis, so that you can start the course smoothly. After installing the python and extra packages, try running the codes in this notebook on your system.

Installing Python

For this course we will frequently use the following python "packages".

• numpy
• scipy
• pandas
• matplotlib
• sklearn
• jupyter notebook

While you can download and install each package from PyPI using PIP, I recommend you to install the Anaconda python distribution, which comes with some popular third party packages (e.g., numpy, scipy, and sklearn). Also, all the code examples and lectures will assume you have installed the Anaconda.

Installing Anaconda

Installing anaconda can be done with just a few clicks.

1. Visit this page and read the instructions.
2. Download the correct installer for your OS and architecture.
   • Window/Linux/OS X
   • 32bit VS 64bit
3. Make sure that you download the Python 3.8 version.
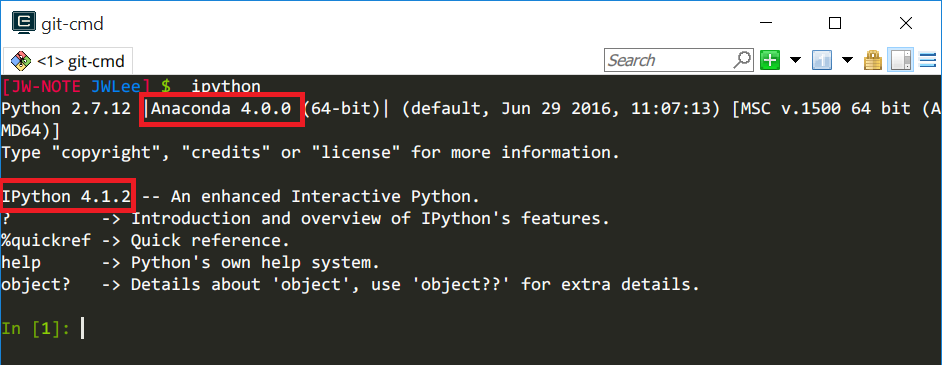
4. After the installation is done, test it by running the ipython.

   ipython

   You should see something like this:
   
   

(Optional) If you already have installed Python or Anaconda

If you've been using Anaconda, then you just need to update the packages to their latest version.

conda update conda
conda update anaconda

If you have python installed on your system and don't want to install anaconda, you can try installing each package using the PIP, a python package installer. If you want to find more about pip, see this page. First, you need to update the pip to the latest version.

pip install --upgrade pip

Once it is done, try installing the following packages:

pip install numpy 
pip install scipy
pip install matplotlib
pip installl sklearn

Jupyter Notebook

Notebook mode

Jupyter notebook has two different mode: command mode and edit mode.

• Edit mode: In edit mode, you can edit the content of a cell.
• Command mode: In command mode, you are not working with a cell but working with the entire document. See (here)[https://jupyter-notebook.readthedocs.io/en/stable/examples/Notebook/Notebook%20Basics.html] for details.

Keyboard shortcuts

When you are in command mode,

• Enter: enter into edit mode
• Shift + Enter: Run cell, select below
• Alt + Enter: Run cell, add a cell below
• Ctrl + Enter: Run cell
• a: add a cell above
• b: add a cell below
• m: change the current cell into a markdown cell
• y: change the current cell into a code cell

When you are in edit mode,

• Esc: Enter into command mode
• Shift + Enter: Run cell, select below
• Alt + Enter: Run cell, add a cell below
• Ctrl + Enter: Run cell
• Tab: auto-complete variable names

Now let's check the version of installed packages.

Q1. Report the versions of packages on your system (5 pts).

Run the following code on your system.

import numpy as np
import scipy
import matplotlib
import sklearn
import pandas as pd

versions = (
    ('numpy', np.__version__),
    ('scipy', scipy.__version__),
    ('matplotlib', matplotlib.__version__),
    ('sklearn', sklearn.__version__),
    ('pandas', pd.__version__)
)

# this syntax is very useful when you concatenate a sequence of words with intervening separators
str = '\n'.join("{0}.version={1}".format(pkgname, ver)
                for (pkgname, ver) in versions)
print(str)

numpy.version=1.18.1
scipy.version=1.4.1
matplotlib.version=3.1.3
sklearn.version=0.21.2
pandas.version=0.25.0

Basics of Python

Hello World

Let's start by introducing how to print out strings in python. To print strings or to see the value stored in a variable, you can use print function. Type the following code in a (code) cell and press shift + enter.

# printing comma separated items
print("Hello CSCI", 213*20)

# better syntax for output formatting
print("Hello {0} {1}".format("CSCI", 213*20))
print("Hello {1} {0}".format("CSCI", 213*20))

# you can also use keyword arguments
print("Hello {deptid} {course_num}".format(deptid="CSCI", course_num=4260))

# positional arguments
print("Hello {} {}".format("CSCI", 4260))


# You can tell the python interpreter to use a specific data type.
# For more about format string sytax, see https://docs.python.org/3.4/library/string.html#formatspec

print("Hello {0:s} {1:d}".format("CSCI", 4260))
# print up to 2 digits after the decimal point
print("Hello {0:s} {1:.2f}".format("CSCI", 4260))
# 10 digit integer (right aligned by default)
print("Hello {0:s} {1:10d}".format("CSCI", 4260))
# to align left
print("Hello {0:s} {1:<10d}".format("CSCI", 4260))

Hello CSCI 4260
Hello CSCI 4260
Hello 4260 CSCI
Hello CSCI 4260
Hello CSCI 4260
Hello CSCI 4260
Hello CSCI 4260.00
Hello CSCI       4260
Hello CSCI 4260      

Basic Data Types and Operations

Python maintains any data you provide as a python object. Based on what you provided, python will automatically determine what objects are used to store them. In python, you don't have to explicitly specify data type when declaring a variable; they are dynamically typed. See the following example, both variables stores the value of 2 but they are stored in different format. One is stored as an integer while the other is as a floating point number.

x = 2
y = 2.0
print("type of x = {},\ttype of y = {}".format(type(x), type(y)))
print("x + 1 = {},\tx -1 = {},\tx * 2 = {},\tx / 4 = {},".format(x+1, x-1, x*2, x/4))

type of x = <class 'int'>,	type of y = <class 'float'>
x + 1 = 3,	x -1 = 1,	x * 2 = 4,	x / 4 = 0.5,

You can also explicitly change one object into the other; this is called type casting. If you want $x$ to be stored as a real number (i.e., float type), you can do so as follows:

print("before the type casting: type(x)=", type(x))
x = float(x)  # explicitly casting into float type
print("after casting int float: type(x)=", type(x))

before the type casting: type(x)= <class 'int'>
after casting int float: type(x)= <class 'float'>

Here is a list of python objects we will be mainly using in this course.

• Numbers: integers (int), real numbers (float)
• Strings: a list of characters
• Containers: a collection of python objects
  • List: orderd collection of objects
  • Dictionary: a set of (key, value) pairs
  • Tuples: immutable list of objects
• Files: handles for file objects (.csv, .txt, etc)

Booleans

Python provides usual boolean operators such as 'logical and', 'logical or", and 'logical not'. See the following example:

mytrue, myfalse = True, False

print("True and False = {}".format(mytrue and myfalse))
print("True or False = {}".format(mytrue or myfalse))
print("not True = {}".format(not mytrue))
print("True xor False = {}".format(mytrue != myfalse))
print("True * 10 = {}".format(mytrue*10))  # True is treated as a value of 1
print("False * 10 = {}".format(myfalse*10))
print("Condition x == y = {}".format(x==y))
print("Condition 1 == 2 = {}".format(1==2))

True and False = False
True or False = True
not True = False
True xor False = True
True * 10 = 10
False * 10 = 0
Condition x == y = True
Condition 1 == 2 = False

Strings

The python string is regarded as a sequence of characters. To declare a string, just enclose the string with either double or single quotation marks. Since they are just list of characters, you can do

• concatenation (combining two strings into another)
• slicing (extracting a substring)
• indexing (access each character by offset)
• looping over a string

To get a better idea, let's see the following examples.

my_string = "CSCI 4260 is cool!"
# concatenation
print("my_string + 'Yeah!' = {}".format(my_string + ' Yeah!'))
# indexing
print("You can access and extract substrings using indices: ", my_string[0:4])
print("The second to the last character is ", my_string[-2])
# length of a string
print("The length of my_string is {}.".format(len(my_string)))
print("Print the string character-by-character: ")
for c in my_string:
    print(c)
    
print("Does my_string contains the word 'CSCI'? ", 'CSCI' in my_string)
print("Does my_string contains the word 'MATH'? ", 'MATH' in my_string)
    
# this will cause an error because strings are immutable (meaning not changeable)
my_string[-1] = '?'

my_string + 'Yeah!' = CSCI 4260 is cool! Yeah!
You can access and extract substrings using indices:  CSCI
The second to the last character is  l
The length of my_string is 18.
Print the string character-by-character: 
C
S
C
I
 
4
2
6
0
 
i
s
 
c
o
o
l
!
Does my_string contains the word 'CSCI'?  True
Does my_string contains the word 'MATH'?  False

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
<ipython-input-6-03227e613496> in <module>
     15 
     16 # this will cause an error because strings are immutable (meaning not changeable)
---> 17 my_string[-1] = '?'

TypeError: 'str' object does not support item assignment

Containers

Python has various built-in containers and a set of functions to manipulate them.

List

The first container type we will look at is the list. A list is a mutable collection of object, which means that it's resizable and can contain different types. To find a complete list of available functions on a list, refer to this document.

# creating a list
mylist = [1, 2, 3, 'red', 'blue', 'green', 112*30]
print(mylist)

# add an item at the end of the list
mylist.append(1)
print(mylist)

# access each item with a (zero-starting) index
print("First item in my list is {0}".format(mylist[0]))
print("The item at index {0} is {1}".format(5, mylist[5]))
# A list can contain another list as an element.
mylist.append([1, 2, 3])
print(mylist)

# remove the i-th element
last_item = mylist.pop(0)
print(mylist)

[1, 2, 3, 'red', 'blue', 'green', 3360]
[1, 2, 3, 'red', 'blue', 'green', 3360, 1]
First item in my list is 1
The item at index 5 is green
[1, 2, 3, 'red', 'blue', 'green', 3360, 1, [1, 2, 3]]
[2, 3, 'red', 'blue', 'green', 3360, 1, [1, 2, 3]]

Slicing: in addition to indexing, python provides an easy way of obtaining a subset of elements, which is called slicing. The syntax for slicing is list[start:end:stride]. Note that the start index is included while the end is not included. This will become clear once you see the following examples.

n = 10
x = range(n)  # this generates (nonnegative) integers smaller than n
print(x)

print(x[1:3])  # the default value for stride is 1
print(x[5:])   # print all the elements whose index is great than or equal to 5
print(x[:5])  # print all the elements whose index is smaller than 5
print(x[::2])  # print every other element
print(x[::3])  # every 3rd element

print(x[-1])  # use a negative index to access elements from the back
print(x[5:-1])
print(x[-5:-1:2])  # what will be the output?

# to reverse a list, you can do 
print(x[::-1])

range(0, 10)
range(1, 3)
range(5, 10)
range(0, 5)
range(0, 10, 2)
range(0, 10, 3)
9
range(5, 9)
range(5, 9, 2)
range(9, -1, -1)

Q2. reverse a string using the list slicing (5 pts).

In python, you can view a string as a list of characters. For example, str="hello" is a list with 5 elements. As you can expect, str[0] == 'h', str[1] == 'e', and so on. Print a reversed string of "hello" using the list slicing. In other words, your output must be "olleh".

# your code goes here (you only need one line of code!)

Looping over a list: When programming in python, we often need to iterate lists (with an index). If you need to access each element with their index,use the built-in enumerate() function.

alphabet = ['a', 'b', 'c', 'd', 'e', 'f']

for letter in alphabet:
    print(letter)
    
print("\nenumerate() returns tuples, where each tuple contains an index and an item")
# if you need their indices as well
for i, letter in enumerate(alphabet):
    print(i, letter)

a
b
c
d
e
f

enumerate() returns tuples, where each tuple contains an index and an item
0 a
1 b
2 c
3 d
4 e
5 f

Dictionaries

A dictionary is useful if you need to store and access the data using key-value pairs. This is a python equivalent of Map in Java.

# the syntax is {key1: value1, key2: value2, ...}
d = {'red': '0xFF0000', 'green': '0x00FF00', 'blue': '0x0000FF'}  # useful for storing mappings

print("red -> {}".format(d['red']))
print("Is pink in d? {}".format('pink' in d))
print("Is green in d? {}".format('green' in d))

# if you try to access an item not in the dictionary, it throws an error
# uncomment the following line and try it by your self.
# print "pink -> {}".format(d['pink'])

# you can avoid this error by specifying a default value
colors = ['red', 'pink', 'green', 'yellow', 'blue']

for color in colors:
    print('{} -> {}'.format(color, d.get(color, 'unknown')))

red -> 0xFF0000
Is pink in d? False
Is green in d? True
red -> 0xFF0000
pink -> unknown
green -> 0x00FF00
yellow -> unknown
blue -> 0x0000FF

Adding and modifying: A new key-value pair will be added if there's no item with the same key. If the key exists, it modifies the existing value.

d['skyblue'] = '0x00FAFF'  # adding a new entry
d['red'] = '0xFFFFFF'      # modifying an existing entry
print(d)

{'red': '0xFFFFFF', 'green': '0x00FF00', 'blue': '0x0000FF', 'skyblue': '0x00FAFF'}

Looping: you iterate the dictionary using a simple for ...in statement.

for color in d:
    print('color {}, code {}'.format(color, d[color]))

color red, code 0xFFFFFF
color green, code 0x00FF00
color blue, code 0x0000FF
color skyblue, code 0x00FAFF

Sets

A list is useful when storing a sequence of heterogeneous objects, but it allows duplicates. Suppose you want to count the number of disticnt words in a movie review dataset. You can use the list for doing this but need to check if the list already contains the word whenever you insert into the list. A set in python is a mutable, unordered, and unique collection of objects. It is designed to reflect the properties of a mathematical set. For more information, see here.

Creation: you can create an empty set using the built-in set() function. Optionally, you can provide an iterable object as an argument to create the set from the elements of existing container.

s = set()  # an empty set
print("An empty set: ", s)

# add an element
s.add(1)
s.add(2)
print("S after adding 2 elements: ", s)

s1 = set(range(2, 10, 2))  # creating a set from a list
print("S1: ", s1)

s2 = set([2, 3, 5, 7])  # set of prime numbers
print("S2: ", s2)

s3 = set([1, 1, 1, 1, 1])  # generate from a list with duplicates
print("S3: ", s3)

An empty set:  set()
S after adding 2 elements:  {1, 2}
S1:  {8, 2, 4, 6}
S2:  {2, 3, 5, 7}
S3:  {1}

Set operations: The set() container comes especially handy when you need to deal with set operations, such as union, intersection, and so on.

# union
print(s1.union(s2))  # {2, 4, 6, 8} U {2, 3, 5, 7}

# intersection
print(s1.intersection(s2))  # {2, 4, 6, 8} /\ {2, 3, 5, 7}

# set difference
print(s2.difference(s1))  # {2, 3, 5, 7} \ {2, 4, 6, 8}

{2, 3, 4, 5, 6, 7, 8}
{2}
{3, 5, 7}

Functions

To define a function in python, you can use def keyword. As an example, let's define fibonacci() function that generates the fibonacci sequence of length n. By definition, the Fibonacci sequence is given by $$ F_n = \begin{cases} 0 & \mbox{ if $n=0$} \\ 1 & \mbox{ if $n=1$} \\ F_{n-1} + F_{n-2} & \mbox{ if $n > 1$.} \end{cases} $$

def fibonacci(n):
    """
    Put your comment here. You comment should explain input parameters 
    and output of the function. For example,
    
    Parameters:
    ------------
    n : integer, the length of fibonacci sequence
    
    Output:
    F : list, fibonacci sequence
    """
    # it's good habit to validate input parameters
    if n < 0:
        print("n must be a non-negative number!")
        
    F = []  # container for the sequence       
    F.append(0)  # F(0) = 0
    
    if n == 0:
        return F
    
    F.append(1)  # F(1) = 0
    
    for i in range(n-1):
        F.append(F[i]+F[i+1])       
        
    return F
    
fib10 =  fibonacci(10)
print(fib10)

[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55]

Be careful with indentation!

Leading spaces and tabs in python are used to determine the indentation depth, which in turn is used to determine the scope (or grouping) of statements.

• For cross-platform compatibility, do not mix space and tabs.
• If you're using an editor, configure it to replace tabs with spaces.

Numpy

Numpy is the fundamental package designed for high performance scientific computing and data analysis. It provides:

• ndarray, an efficient implementation of multi-dimensional array object providing _vectorized) arithmetic operations and broadcasting capabilities
• Linear algebra, for example, matrix multiplication, eigen value decomposition, SVD, and so on
• Statistical tools for handling probability distributions
• Random number generation To use numpy, start your code with the following import statement.

  import numpy as np
  

Array

Numpy array is an efficient container for large datasets in python that contains homogeneous data, which means all the elments must be of the same type.

Creation: There are two ways to create ndarray object: create an empty array or create it from an existing array.

import numpy as np

arr1 = np.empty(10)  # create an empty 1d array of length 10
print(arr1)          # it's created but not intialized
# you should always intialize them before accessing them

# create and intialize each entry with zero values
arr2 = np.zeros((2, 2)) # 2d array of shape (2, 2)
print("\n2D array with shape {}".format(arr2.shape))
print(arr2)

# create and intialize with ones
arr3 = np.ones((3, 3, 3)) 
print(arr3)

# creating from an existing container
mylist = [1, 2, 3, 4, 5, 6]
myarray = np.array(mylist)
print(myarray)

[3.31023983e-322 3.55727265e-322 4.66839074e-313 0.00000000e+000
 0.00000000e+000 0.00000000e+000 6.89772896e-307 1.11261162e-306
 8.34443015e-308 3.91792476e-317]

2D array with shape (2, 2)
[[0. 0.]
 [0. 0.]]
[[[1. 1. 1.]
  [1. 1. 1.]
  [1. 1. 1.]]

 [[1. 1. 1.]
  [1. 1. 1.]
  [1. 1. 1.]]

 [[1. 1. 1.]
  [1. 1. 1.]
  [1. 1. 1.]]]
[1 2 3 4 5 6]

Slicing: you can apply the slicing on a numpy array using a similar sytax to that of python's list.

# you can also use the slicing operator
print(myarray[3:])
print(myarray[-1])

[4 5 6]
6

Boolean indexing: Suppose you want to select the entries satisfying a certain condition. If you express any arithmetic operations on numpy array, they are vectorized, meaning that each operation is propagated to each element. In the following example, the comparison operation is expressed between an array and a scalar. This operation is propagated to each element, and the result will be vectorized.

# boolean indexing

print(myarray)

# if you want to access only the element greater than 2, you can express it as
print(myarray > 2)

# the result is a vector of booleans, and we can use this boolean array as indices
print(myarray[myarray > 2])

# modifying only entries satisfying the condition
myarray[myarray > 2] =0
print(myarray)

[1 2 3 4 5 6]
[False False  True  True  True  True]
[3 4 5 6]
[1 2 0 0 0 0]

If you want to create an array having the same shape with an existing array, you can use ones_like(), zeros_like(), empty_like().

x = np.array([[1, 2], [3, 4]])
print("x has the shape", x.shape)

y = np.zeros_like(x)
print("y must have the same shape with x,", y.shape)

x has the shape (2, 2)
y must have the same shape with x, (2, 2)

So far, we didn't specify data types when creating an array. By default, numpy will try to infer the type from the element, but it's safer to specify the type explicitly.

arr = np.array([1, 2, 3, 4, 5])  # didn't specify a type
print("guessed data type =", arr.dtype)

# this can be problematic if you want to do arithmetic operations on them
arr = arr / 2   # divide each element by 2 (what will be the result?)
print(arr.dtype)  # notice the type has been chnaged       

# You may expect that x = x / 2 and x /= 2 are the same, but the follwing
# code will occur an error. Uncomment the next line and execute it.
# arr = np.array([1, 2, 3, 4, 5])
# arr /= 2
# print(arr)

# repeat the above but this time with type specified
arr = np.array([1, 2, 3, 4, 5], dtype=np.float32)
arr /= 2  # divide by 2
print(arr)

guessed data type = int32
float64
[0.5 1.  1.5 2.  2.5]

Q3. Explain why the commented line of code in the above cell causes an error (5pts).

(hint: the line a = a / 2 sequentially performs division and assignment but a /= 2 doesn't)

Broadcasting

Broadcating in numpy allows you to perform arithmetic operations on arrays efficiently. By default, operations between two numpy arrays are element-wise. For illustration, let's define two arrays.

X = np.random.randn(2, 2)
Y = np.random.randn(2, 2)
print(X)
print(Y)
print("X + Y = \n", X + Y)  # element-wise addition

[[-1.04235898 -0.67119513]
 [ 0.64032331 -1.44064146]]
[[-1.61356232  0.1396451 ]
 [-0.59449651 -1.04062881]]
X + Y = 
 [[-2.6559213  -0.53155003]
 [ 0.0458268  -2.48127027]]

Often, we want to perform an operation between a vector and matrix (i.e., between two arrays with different shapes). Let's take an example.

X = np.array([[1, 2, 3], [4, 5, 6]])
print(X)
Y = np.array([-1, 0, 1])

# What would be the result of X+Y?
X + Y

[[1 2 3]
 [4 5 6]]

array([[0, 2, 4],
       [3, 5, 7]])

To understand the above result, you need to understand how broadcasting in python works. When performing an operation on two numpy arrays, python first inspect the shape of each array. In our example,

print("X's shape is ", X.shape, " and Y's shape is ", Y.shape, ".")

X's shape is  (2, 3)  and Y's shape is  (3,) .

The python will notice that one is a 2D array while the other is a 1D array.

1. The numpy tries to pad the one with smaller dimensionality with 1 from the left side. In other words, numpy will change the shape of Y to (1, 3).
2. Then numpy will try to match the shape of two arrays by inspecting the size of each dimension.
   • For the first dimension, the size of X is 2 while that of Y is 1. If the size of one array is 1, it tries to stretch to match the other array's size. In our example, Y's first dimension is stretched to the size of 2 to match that of X by replicating elements vertically. In other words, Y becomes $$ Y = \begin{bmatrix} -1 & 0 & 1 \\ -1 & 0 & 1 \end{bmatrix}. $$
   • For the second dimension, the size of both arrays is 3. So, numpy performs the element-wise addition between the following two arrays. $$ X + Y = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} + \begin{bmatrix} -1 & 0 & 1 \end{bmatrix} \Rightarrow \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} + \begin{bmatrix} -1 & 0 & 1 \\ -1 & 0 & 1 \end{bmatrix} $$

Let's look at another example.

X = np.array([[1, 2, 3], [4, 5, 6]])
Y = np.array([1, 2])

# Can you guess the results of X+Y?

We know the shapes of X and Y are (2, 3) and (2,), respectively. Since their dimensionality doesn't match, it will pad Y to have the shape (1, 2). Let's compare their sizes dimension by dimension. The sizes of first dimension do not match: 2 and 1, but numpy will try to stretch the size of Y to 2 to match the X's size. For the second dimension, we have a mismatch again: 3 VS 2. However, neither X nor Y has the size 1, so numpy will throw an error as there's no way it can match the sizes of two arrays. See the error message below!

X + Y

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
<ipython-input-51-e4a642f73c42> in <module>
----> 1 X + Y

ValueError: operands could not be broadcast together with shapes (2,3) (2,) 

Why using numpy arrays: ndarray is memory efficient and provides fast numerical operations. The following examples just create a sequence $\{x^2: i=1, 2, \ldots, 1000\}$.

# python's list
a = range(1, 1001)
%timeit [i**2 for i in a]

378 µs ± 7.41 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)

# repeat the same using a numpy array
a = np.arange(1, 1001)
%timeit a**2

1.48 µs ± 14.6 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)

Saving and Loading Text Files

A frequent task you will be doing throught the semester is to load data from text files. pandas package provides read_csv() and read_table() functions for easy loading of data from files. Numpy also provides np.loadtxt() function to load data directly into numpy array.

# generate a random data following Gaussian distribution
x = np.random.randn(5, 5) 
print(x)
# to save an numpy array into a text file
np.savetxt('myarray.out', x, delimiter=',')

# load the data from a text file 
y = np.loadtxt('myarray.out', delimiter=',')
print(y)

[[-1.58490594  0.41165671  0.63350179 -0.3401466  -0.67823426]
 [ 1.21955582  0.17596789 -1.37760864 -0.09794624 -2.26611511]
 [ 2.33058364 -0.44889901  0.40046212 -0.73817591  0.09498042]
 [-0.09215983  0.93309669 -0.81667184  0.21208477  1.30212128]
 [-0.92334705 -0.81187776 -0.59147425  1.14260113 -0.54246467]]
[[-1.58490594  0.41165671  0.63350179 -0.3401466  -0.67823426]
 [ 1.21955582  0.17596789 -1.37760864 -0.09794624 -2.26611511]
 [ 2.33058364 -0.44889901  0.40046212 -0.73817591  0.09498042]
 [-0.09215983  0.93309669 -0.81667184  0.21208477  1.30212128]
 [-0.92334705 -0.81187776 -0.59147425  1.14260113 -0.54246467]]

Random Number Generation

To generate random numbers, you can use numpy.random module. Here is a list of functions provided by the module (as always, refer to the python documentation for more details).

Function	Description
np.random.randn()	draw samples from a standard normal
np.random.rand()	draw samples from a uniform distribution
np.random.binomial()	draw samples from a binomial distribution
np.random.uniform()	draw samples from a uniform[0,1) distribution
np.random.gamma()	draw samples from a gamma distribution
np.random.shuffle()	randomly permute a sequence in place
np.random.choice()	generate a random sample from an array

Our first plot

To check if the matplotlib is correctly installed, we will draw 10,000 random samples from the Gaussian distribution with mean 0 and standard deviation 1, i.e., standard normal distribution, and draw a histogram. If you are not sure what the following code is doing, don't worry; we will comeback to this again. You may want to play with this plot by changing the value of nsamples and nbins.

# you need to include this line to have the matplotlib diplay plots inline
%matplotlib inline
import matplotlib.pyplot as plt

# draw 10,000 random samples from the standard normal distribution
nsamples = 10000
nbins = 20
x = np.random.randn(nsamples)
# build a histogram (number of bins = 20)
bins, edges, patches = plt.hist(x, bins=nbins, facecolor='blue')

plt.xlabel('x')
plt.ylabel('Frequency')
plt.grid(True)
plt.show()

Q3. Write a function that simulates a (biased) coin flip (10 pts).

A biased coin flip can be modeled as a random variable that follows Bernoulli distribution. Let $X$ be a random varaible that takes the value of 1 if the coin flip ends with "head" and 0 otherwise. Mathematically, this can be written as $X \sim \mathsf{Bernoulli}(p)$, meaning $$ X = \begin{cases} 1 & \mbox{ with probability $p$} \\ 0 & \mbox{ with probability $1-p$.} \end{cases} $$

def coin_flip(p):
    """
    This function simulates a biased coin flip. Generate a random number 
    from uniform[0, 1), and return 1 if the number is less than or equal to p 
    and 0  otherwise.
    
    Parameters
    ---------------
    p: float, probability of getting a head
    
    Returns
    --------
    X: bernoulli random variable (either 0 or 1)
    """
    #######################
    # your code goes here #
    #######################
    
    return X

# we're going to throw this coin n times
p = 0.3
n = 10

experiment = np.array([coin_flip(p) for i in range(n)])

# how many heads did we have?
n_head = np.count_nonzero(experiment == 1)
print("probability of getting head = {:.2f}".format(float(n_head)/n))

What did we do?

Our population (coin flips) is modeled by a Bernoulli random variable with the unknown parameter $p$, the probability of head. To estimate the the parameter $p$, we collected a random sample of size $n=10$ and estimated $p$ by simply counting number of heads and dividing it by $n$ (to make a probability). Is our estimate for $p$ close enough to the true value of 0.3? With $n=10$, probably our estimate is very inaccurate. Let's see what happens as we increase the sample size $n$.

sample_sizes = [10, 30, 50, 70, 100, 500, 1000, 5000, 10000, 20000, 50000]
estimates = []

# repeat the above procedure for different values of n
for n in sample_sizes:
    experiment = np.array([coin_flip(p) for i in range(n)])
    n_head = np.count_nonzero(experiment == 1)
    est_p = float(n_head) / n
    estimates.append(est_p)
    
# draw a plot showing how our estimate changes as we increase the sample size
plt.semilogx(sample_sizes, estimates, 'C0-', label='estimate')
plt.axhline(p, c='C1', ls='--', label='true p')
plt.xlabel('sample size (n)')
plt.ylabel('Probability of heads')
plt.legend(loc='best')

Try executing this cell a few times! What do you observe?

It is known that the sum of $n$ independent Bernoulli random variables follows a Binomial distribution. Formally, $$ \begin{equation} Y = X_1 + X_2 + \cdots + X_n \sim \mathsf{Binomial}(n, p)\,, \end{equation} $$ where $X_i \sim \mathsf{Bernoulli}(p)$ for $i=1, \ldots, n$.

Q4. Simulate n coin flips t times and draw a histogram (5 pts).

The n_coin_flips() function below returns a number of heads in $n$ coin flips, which follows a binomial distribution. That is, n_head$\sim \mathsf{Binomial}(n, p)$. To generate a sample of size $t$, run the n_coin_flips() function $t$ times and build a histogram on the sample. You can use plt.hist() to draw a histogram. For input parameters and outputs, see here.

def n_coin_flips(n, p):
    """
    Parameters:
    ---------------------
    n: int, number of coin flips
    p: probability of getting head
    
    Returns
    -----------------
    n_head: int, number of heads
    """
    experiment = np.array([coin_flip(p) for i in range(n)])
    n_head = np.count_nonzero(experiment == 1)
    
    return n_head

Here's the test code for your implemenation of n_coin_flips() function.

# sample n_head t times
t = 1000
n = 10

# run n_coin_flips() t times
x = [n_coin_flips(n, p) for i in range(t)]

# compute mean and standard deviation of x
# for a list of statistical function in numpy, see 
# https://docs.scipy.org/doc/numpy-1.13.0/reference/routines.statistics.html
x_mean =  ### Which numpy function does compute the mean of the elements in the given array?
x_std =   ### Which numpy function can you use to compute their standard deviation?

# Do they match with analytical solution?
# FYI, when Y ~ binomial(n, p), its mean is np and variance is np(1-p).
print("sample_mean={:5.3f}, analytical mean={:5.3f}".format(x_mean, n*p))
print("sample std.={:.5f}, analytical std={:.5f}".format(x_std, np.sqrt(n*p*(1-p))))

# your code for drawing a histogram goes here
# set bins=8 and density=True

# you can add an analytical pmf using the following code
from scipy.stats import binom

y = np.arange(8)
pmf = binom.pmf(y, n, p)
plt.plot(y, pmf)

sample_mean=2.934, analytical mean=3.000
sample std.=1.47636, analytical std=1.44914

[<matplotlib.lines.Line2D at 0xeed9dd8>]

Timeit

When you are writing a program, you may wonder how fast or slow a particular piece of code is. %timeit is a function for doing this. The following code shows 3 different ways to calculate the sum of squares of numbers in a list. $$ SS = \sum_{i=1}^n x[i]^2 $$

def square(x):
    return (x**2)

def func_A(x):
    n = len(x)
    SS = 0
    
    for i in range(n):
        SS += (x[i]*x[i])
        
    return SS

def func_B(x):    
    return sum(map(square, x))

def func_C(x):
    return np.sum(np.square(x))

# create a list of length 100
x = np.arange(1, 51)

print("func_A(x)=", func_A(x))
print("func_B(x)=", func_B(x))
print("func_C(x)=", func_C(x))

# now check which function is the fastest
%timeit func_A(x)
%timeit func_B(x)
%timeit func_C(x)

func_A(x)= 42925
func_B(x)= 42925
func_C(x)= 42925
100000 loops, best of 3: 12.8 µs per loop
100000 loops, best of 3: 15.9 µs per loop
The slowest run took 9.84 times longer than the fastest. This could mean that an intermediate result is being cached.
100000 loops, best of 3: 2.57 µs per loop